Answers to those Doggone Thermal Design Questions
By Tony Kordyban
Copyright by Tony Kordyban 2003
Dear Tony,
In your October 2003 discussion of the piezoelectric fan in a cell phone you stated that fixed total power and a sealed phone with no holes prohibit the fan from lowering the case temperature. Let’s assume the piezoelectric fan does in fact perfectly mix the internal air to its average temperature (no hot spots remain). The average temperature difference between the internal air near the case wall to ambient air would thus be greater. With a constant external convection coefficient, the heat transfer from inside
the case to ambient air should then increase, therefore lowering the case temperature. Let me know if there are any ‘holes’ in this theory.
Another fan in Seattle
Dear Another,
This is a wonderful question. It sounds so simple at first, but when you try to explain why the answer is so obvious, you realize you have no idea what the real answer is. So you have to sit down with a paper and pencil and figure it out, and you learn something. I love those kinds of questions. They give me something to think about when my wife is telling me about her genealogy hobby.
Before I answer your question, I should explain the original problem. A Purdue research lab came up with a fan tiny enough to fit inside a cell phone. The publicity video claimed that it would fix the problem of a cell phone being too hot to hold against your ear. I disagreed, saying that an internal fan could not fix that particular problem. An internal fan could lower the component temperatures inside the phone, but it could do nothing to lower the outer skin temperature of the phone.
This is not exactly true.
I had assumed that the cell phone frying the woman’s ear was hot all over — it didn’t have just one small hot spot. If there were just one small offending hot spot, then an internal fan could stir the air inside, cooling the hot spot, and warming up the rest of the phone, averaging the high temperature of the hot spot with the relatively cool spots in the rest of the phone. If that averaged temperature were low enough to be comfortable against one’s face, then the internal fan really could solve the problem.
But if the entire surface of the cell phone case is too hot, then an internal fan is useless. Assuming that the skin temperature is uniform, and that the convective heat transfer coefficient (h) is also uniform all along the surface of the phone, then the outside skin temperature of the phone is given by:
T skin = T ambient + Q / (h A)
where Q is the total heat generated inside the phone, and A is the surface area of the outside of the phone. Nowhere in this equation does it mention what is happening inside the phone. The thermal resistance between the internal air and the skin is irrelevant. (It is irrelevant to the outside skin temperature, but not to the component temperatures inside.)
If the heat generated inside is distributed evenly, then this is the situation you will get. The skin temperature, and the heat transfer from every spot on the skin is uniform, and you can use this simple equation to calculate the skin temperature. This is what can’t be fixed by an internal fan. (Once again, an internal fan will reduce component temperatures, but won’t help the woman with the burning ear lobe!)
That answers part of your question. Yes, having a uniform temperature is beneficial because you have lowered the thermal resistance between the internal air and the external air. It does this because the heat now conducts through a larger cross-sectional area of the skin, which gives a lower conduction resistance. That does not reduce outside skin temperature, though. It only reduces internal air temperature, and internal component temperature.
I surmise that your gut feeling about uniform temperature being the “optimum” comes from your experience with heat sinks. We try (with good reason) to make the base and fins of heat sinks thick, so that the whole heat sink is at a uniform temperature. You get the most heat transfer for the lowest temperature rise (put simply, minimum thermal resistance) if all the surfaces of the sink are close to the same temperature.
But is uniform skin temperature the optimum for heat transfer from a sealed case like a cell phone?
That is the question that seemed to have an obvious answer to me. But the more I thought about it, the less obvious the answer became.
It is easy to figure out the skin temperature if the heat, temperature, and h are constant everywhere. It is not so simple to know what is going on if the skin temperature varies from place to place. For one thing, in natural convection, h depends on the temperature difference between the surface and the air. After all, it is the heat that drives the air flow, so the bigger the temperature difference, the stronger the driving force that carries the heat away. And we can’t neglect radiation either, considering that natural convection can be very weak. With radiation depending on the fourth power of absolute skin temperature, it is hard to have a good feeling for what happens when you have mixture of cool spots and hot spots.
So I abandoned my gut feelings (my friends say I have no guts anyway) and did some calculating. I wanted to answer the question: Which surface dissipates more heat: one with a uniform temperature 20°C above ambient, or one with non-uniform temperature, that averages out to 20°C above ambient?
Instead of a complicated cell phone surface, let’s simplify it to a flat plate of similar size. Then let’s divide that plate into 11 or so equal patches. We can assign different temperatures and corresponding values of h to each patch, and then add up how much heat transfer we get. Which gives off more heat by natural convection, a uniform temperature plate, or a non-uniform plate with the same average temperature?
In natural convection, h varies with geometry and temperature difference. What can we use to vary h as the temperature changes from place to place?
Maybe what I picked isn’t accurate, but it should give us the right amount of variation in h with temperature rise. I chose a textbook correlation for natural convection from a flat plate:
Nu = 0.59 (Gr Pr)0.25
Don’t panic. Those are our old nemeses, the Nusselt, Grashof and Prandtl numbers. Here is the same equation with variables you might recognize:
h = (k/L) Pr 0.25 (g b (Tsurface – Tair) L3 / n 2 )0.25
k is the conductivity of air
L is the length of the patch
Pr is the Prandtl number, a property of air
g is the acceleration of gravity
b is the expansivity of air
(Tsurface – Tair) is the temperature difference between the surface and air
n is the viscosity of air
The important thing to note is that h goes up when the surface temperature goes up.
If we know h, then for each patch we can calculate the heat lost by convection from
Q convection = h A patch (T patch – T ambient )
A pretty good estimate of the radiation lost from each patch is given by:
Q radiation = s e A patch {(T patch + 273K)4 – (T ambient + 273K)4}
where s is the Stefan-Boltzman constant, and e is the emissivity of the surface.
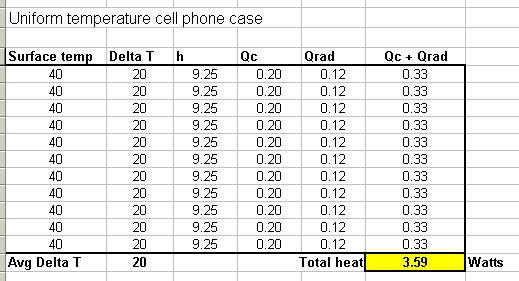
Go ahead and do the calculations with me if you want, but here are the results for a plate that is 300 mm x 150 mm, with emissivity of 0.9. ( I assumed heat transfer from one side of the plate only.) Ambient is 20°C, and each plate has a temperature distribution that averages to a temperature rise of 20°C.
With uniform temperature, each patch gives off uniform convection and uniform radiation. Is this really the best that can be done with an average temperature rise of 20°C?
Here is the result with a linear rise in temperature from one end of the plate to the other, averaging out to 20°C rise.
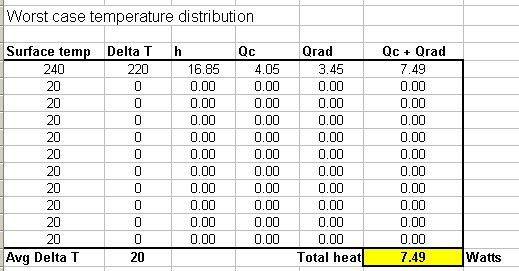
This non-uniform temperature distribution actually gives off more heat than the uniform temperature plate. That is because h and radiation both go up with temperature difference. But the difference is not very large (about 6%). What happens if he have one really bad hot spot?
This was a surprising result to me. The “poor” temperature distribution with one very bad hot spot gives off nearly twice the heat as the uniform temperature plate with the same average temperature rise.
What lessons should we get from these three simple spreadsheet calculations? Should we design cell phones with all the power concentrated in one tiny spot?
I don’t recommend that, because although you would have an excellent heat transfer rate at that spot, you would also have very high component temperatures. And such a hot spot would instantly brand the unwitting customer with your company logo right on her face. Such a scar might be great free advertising, but would not look good to a jury.
The lesson I learned is that for natural convection, it is not the average temperature that counts, but the temperature distribution.
My example assumes that the plate (or cell phone case) is a very poor conductor of heat, so hot spots would not tend to even out by spreading heat in the wall thickness.
But this does point out the very real possibility that if we put a fan inside a cell phone to get rid of a hot spot, we might actually increase the internal temperatures overall. By making the skin temperature more uniform, we might be increasing the overall thermal resistance between the skin and the ambient. The average skin temperature might actually be higher than without the internal fan.
I love these types of paradoxical questions. You might have to work out these calculations yourself before you can believe me. Try them. It is very easy in a spreadsheet. It is much easier to do the calculations than to reason out the answer in you head.
How can adding a fan make the average temperature go up? Isn’t cooling electronics fun?
—————————————————————————————————————
Isn’t Everything He Knows Wrong, Too?
The straight dope on Tony Kordyban
Tony Kordyban has been an engineer in the field of electronics cooling for different telecom and power supply companies (who can keep track when they change names so frequently?) for the last twenty years. Maybe that doesn’t make him an expert in heat transfer theory, but it has certainly gained him a lot of experience in the ways NOT to cool electronics. He does have some book-learnin’, with a BS in Mechanical Engineering from the University of Detroit (motto:Detroit— no place for wimps) and a Masters in Mechanical Engineering from Stanford (motto: shouldn’t Nobels count more than Rose Bowls?)
In those twenty years Tony has come to the conclusion that a lot of the common practices of electronics cooling are full of baloney. He has run into so much nonsense in the field that he has found it easier to just assume “everything you know is wrong” (from the comedy album by Firesign Theatre), and to question everything against the basic principles of heat transfer theory.
Tony has been collecting case studies of the wrong way to cool electronics, using them to educate the cooling masses, applying humor as the sugar to help the medicine go down. These have been published recently by the ASME Press in a book called, “Hot Air Rises and Heat Sinks: Everything You Know About Cooling Electronics Is Wrong.” It is available direct from ASME Press at 1-800-843-2763 or at their web site at http://www.asme.org/pubs/asmepress, Order Number 800741.