Answers to those Doggone Thermal Design Questions
By Tony Kordyban
Copyright by Tony Kordyban 2002
Dear Mr. Everything Wrong,
I think I know how to calculate the heat dissipation from most kinds of electronics. You just measure the electric power going into the chassis, and pretty much all of it gets converted into heat. With power getting higher and higher all the time, our customers are getting picky about accurate values for heat dissipation. They need it so they can size their room air conditioning. It used to be OK to just tell them the fuse rating for the system, but now they want a realistic number. The cost of the electricity and the air conditioning are getting so high that customers now care about them. They even compare our heat dissipation against our competitors.
That leads up to my question: How much of the electric power that is drawn by the cooling fans gets converted into heat? After all, some of the electricity gets converted into useful work in pushing the air through the box, so I don’t think that 100% of the electrical power gets changed into heat. So what is the “efficiency” of a fan? 20%? 80%? Is there some way to calculate it?
The fans in my chassis draw 500 watts to cool electronics that dissipate 2500 watts, so I can’t just ignore what might be 20% of the power.
Going in Circles in Dupont Circle
Dear Going,
When I first read your question, I thought I was in deep trouble. One way to answer it is to look at the details of the fans, and try to calculate the efficiency of the electric motor, by looking at things like the resistive loss in the coils and the friction loss in the bearings. Then you could analyze the aerodynamic losses of the fan blades in motion. But I was never very good at rotating cylindrical coordinate systems. So I fell back on a very common trick from the world of thermodynamics.
When the details of a process are too tricky to figure out, you just draw a boundary line around the whole thing and do an energy balance. For any closed boundary, the sum of the energy going in plus the energy going out plus the energy generated inside have to add up to zero (if you get the signs right, of course.) Your question has two different answers, depending on where you draw the boundary line of your system.
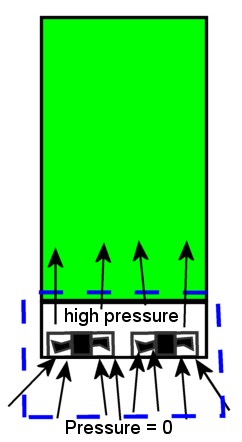Just for laughs, let’s draw the boundary of our system to be the outer edges of your fan tray. I have sketched it here, with the dotted blue line representing the boundary that we will perform the energy balance on.
In this case you have electric power going in through the boundary to drive the fans. Then there is the energy of the moving stream of air crossing the system boundaries. The air flowing into the inlet of the fans is at low pressure, and the flow leaving the exit of the fan tray is at the same flow rate, but it is at some higher pressure because of the work added by the fans.
It is very simple to calculate the work done on a stream of fluid across a change in pressure.
Power = (change in pressure)(volumetric flow rate)
It is not too hard to measure the pressure on the exhaust side of the fans, and you can also measure the total flow rate. You could even estimate these values from the fan performance curve and your system resistance curve. Then you subtract that from the electrical power into the fan tray and you get the amount of power that is converted to heat.
This little exercise is interesting if you want to estimate how much of the fan power is going to heat the air stream that is cooling your circuit boards. A 500W fan tray could conceivably add a couple of degrees C to the inlet air. But this method will allow you to know how much of that 500W turns into heat and how much into pressurized air flow.
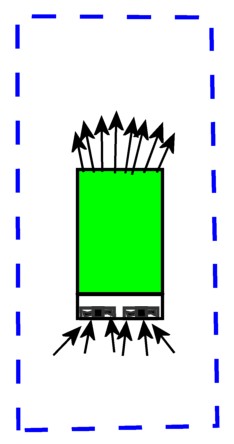But that isn’t the question you asked me, is it? You don’t want to know how much the fans contribute to air temperature rise inside your shelf. You want to know how much the fans contribute to air temperature rise inside the room where it is installed. That question requires us to draw the system boundary a little bit bigger, to something about the size of the room itself. And that will cause the answer to change.
You still have the electrical power crossing into the boundary to drive the fans. But if you draw the boundary a meter or so away from the inlet and outlet vents, you most likely don’t have any air flow crossing the boundary, at least none generated by the fans. The pressure all around the boundary is essentially zero, and any velocity that the air stream had when it left the exit vent of the chassis has pretty much spread out and dissipated into the large volume of air in the room.
As far as the room knows, that work to accelerate the air against a pressure drop never happened.
So where did that work go?
It went where all of our “losses” go — it changed from macroscopic motion of air molecules into
microscopic molecular motion — heat energy. The useful work generated by your fans got done being useful soon after it exhausted into the room. It is not doing any work in the room. It succumbed to viscosity and changed from velocity and pressure to temperature.
So the sad but simple answer to your question is that 100% of the fan power is converted to heat, as far as your customer’s air conditioning system is concerned. Even the audible noise, unless they leave the windows open and let the sound power transmit to the outside world, where it would heat someone else’s air.
—————————————————————————————————————
Dear TK,
Where the heck did you get that expression for the work done by a fan? I thought that work was defined as a force acting through a distance.
By the way, cool book! When are you coming out with a sequel?
Jim-Bob from Walton’s Mountain
Dear Jim,
You thought right. Work is force acting through a distance, or, as put formally in my 8th grade General Science book:
Work = force x distance
Since in the field of electronics cooling we usually talk about power and power dissipation and heat transfer rate, let’s define power:
Power = work/time or Power = (force x distance)/time
So how do you apply that to fluid (like air) flowing through a pipe (or an electronics chassis)? What you have is fluid flowing with a velocity from a region of one pressure to a region of another pressure. It takes power to force a fluid to move through a resistance, such as a box full of circuit boards. The force acting to make the fluid move is related to the pressure difference:
Force = pressure x area
where area is the cross-sectional area of the flow duct. So you could say that
Power = (pressure x area x distance)/time
or you could re-arrange the terms a little bit and get
Power = pressure x area x (distance/time)
But what is distance/time? That is just velocity. And what is velocity x area? That is the volumetric air flow rate through the box. So just by juggling a few terms around, I have shown that your formula for work is the same as:
Power = pressure x volumetric flow rate
If you use Pascals for pressure and cubic meters per second for flow rate you should even get watts for your power value. Proving that is your homework assignment.
(And in case you crack open a fluids textbook during your homework and notice some terms missing from my formula, yes, I am neglecting potential energy due to a change in elevation.)
As to a sequel to “Hot Air Rises and Heat Sinks”, that will be a little tougher to derive. I have a volume of material that could be used for such a sequel, but it will take a lot of pressure to get it flowing against the resistance of my publisher. A few e-mails to ASME Press couldn’t hurt, but the kind of pressure they respond to better is when somebody buys a whole bunch of the original book. Try that first.
2012 UPDATE: That pressure did materialize, and a sequel, “More Hot Air,” was published in 2005. See the Books page for where to get a copy.
—————————————————————————————————————
Isn’t Everything He Knows Wrong, Too?
The straight dope on Tony Kordyban
Tony Kordyban has been an engineer in the field of electronics cooling for different telecom and power supply companies (who can keep track when they change names so frequently?) for the last twenty years. Maybe that doesn’t make him an expert in heat transfer theory, but it has certainly gained him a lot of experience in the ways NOT to cool electronics. He does have some book-learnin’, with a BS in Mechanical Engineering from the University of Detroit (motto:Detroit— no place for wimps) and a Masters in Mechanical Engineering from Stanford (motto: shouldn’t Nobels count more than Rose Bowls?)
In those twenty years Tony has come to the conclusion that a lot of the common practices of electronics cooling are full of baloney. He has run into so much nonsense in the field that he has found it easier to just assume “everything you know is wrong” (from the comedy album by Firesign Theatre), and to question everything against the basic principles of heat transfer theory.
Tony has been collecting case studies of the wrong way to cool electronics, using them to educate the cooling masses, applying humor as the sugar to help the medicine go down. These have been published recently by the ASME Press in a book called, “Hot Air Rises and Heat Sinks: Everything You Know About Cooling Electronics Is Wrong.” It is available direct from ASME Press at 1-800-843-2763 or at their web site at http://www.asme.org/pubs/asmepress, Order Number 800741.