Answers to those Doggone Thermal Design Questions
By Tony Kordyban
Copyright by Tony Kordyban 2001
Dear Thermal Guru,
I recently had to attach a thermocouple to the lead of a component. I recalled a story about a guy named Herbie who had done something similar and ended up with erroneous temperature measurements (because the thermocouple wires picked up voltage from the component lead). To avoid repeating Herbie’s mistake I decided to apply a bit of Kapton tape to the lead before attaching my wire, with the understanding that the Kapton would also affect the measurements, although (I hoped) in a minor way.
My tests showed that the component was very close to its operating limit, so I needed to know how big an error the Kapton tape might have introduced. So I computed the thermal resistance of the tape using the trusty formula R = t / (k*A). My result was about 100 deg C/ watt (see details in next paragraph), and the component was dissipating 1 watt. That seemed to imply a 100 deg C rise across the Kapton, and that just didn’t seem right.
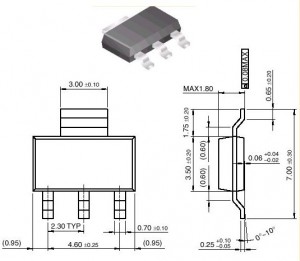
Calculation details: the component was in a SOT-223 package; I assumed the Kapton tape was the same size as the lead (see dimension in the figure below). The Kapton was .0025 inch thick; I used k = 0.12 W/mK (source: the DuPont web site); I neglected the adhesive and assumed that there was no air trapped under the tape.
I know that I’m using a 1-D conduction approximation, which may not be great, but then I don’t need a computer to solve it. But is it wrong to use the full package power dissipation of 1 watt for the heat passing through the Kapton tape? What is the right thing to do?
Baffled in Boston
Dear Baffled,
At first I thought, this guy must be nuts, thinking that all the heat generated in his component would pass through the single lead that he happened to be measuring the temperature of. There must be at least 23 other leads on the package, so the power going through any one of them must be pretty small. Then I looked at Figure 1, and now I understand what you are talking about. So I’ll reserve judgment on your nuttiness for now.
Figure 1. SOT 223 geometry
This package looks suspicious to me. Why is one lead so much bigger and fatter than the other three? My guess is that the fat one is meant to be the thermal path from the die to the printed circuit board (PCB), and might be pretty well connected to the die. The three smaller leads are probably only connected to the die by bond wires. So your assumption that most of the 1 watt generated inside the package comes out through that lead might be a pretty good one.
I checked your math, and I get a thermal resistance of about 100 deg C/watt for Kapton tape on top of the big fat lead. Now the big question is, does all of that 1 watt in the lead come out through the top surface where the tape is?
Obviously, the end of the lead is soldered to a copper pad on the PCB, and some portion of that 1 watt will conduct through the lead and into the board. So that gives at least two major paths for heat to get out of the lead::
- conduction into the PCB
- convection to the air from the top surface
What we need to do is get a sense of how much flows through each path. If we assume that the PCB and the air are at about the same temperature, then we can simplify this into a two resistor network, with the two resistors in parallel with each other. In that case, we can estimate the heat flow into the air with this equation:
Heat Flow air / Heat Flow total = Resistance PCB / ( Resistance PCB + Resistance air )
So where do you get these resistances? The conduction resistance formula you have already given me:
Resistance PCB = t / ( k Acs)
where t is the path length of conduction, k is the conductivity of the material (the component lead), and Acs is the cross-sectional area of the path (the lead). If I assume a conductivity of about 100 W/mK for the lead (up to 400 W/mK if I assume pure copper), and given the lead dimensions in Figure 1, I get a thermal resistance for heat conducting into the PCB of about 27 deg C/ watt.
What about the resistance to the air from the top surface? That depends on the speed of the air and turbulence and so on. But the resistance formula is simple:
Resistance air = 1 / (h A)
where h is the convection coefficient and A is the surface area of the top of the lead. You didn’t mention whether you have natural convection or fan cooling. I am going to assume a value of h for fan cooling with fairly low velocity — which is typical for electronic assemblies. I pick h = 20 W/square meter/K.
Using the lead top surface area from Figure 1, and h = 20, I estimate the resistance from the lead to the air to be about 8300 deg C/watt. If h is higher, the resistance will be lower, of course. You can pick a value that seems right for your situation.
Plugging these resistances into the first equation, I find that the heat flow through the top surface of the lead is about 0.32% of the total power entering the lead. With device power at 1 watt, the heat passing through the Kapton tape is about 0.0032 watts. Given that the thermal resistance of the tape is 100 deg C/watt, then the temperature difference across the tape is about 0.32 deg C.
That agrees a lot better with my gut feeling about Kapton tape than 100 degrees C would. How does your gut feel?
—————————————————————————————————————
Dear Tony,
In your November 2001 article about humidity, air density, and its affect on heat transfer, you made a small boo-boo. You said that humid air was denser than dry air, and would have better heat transfer because of the increased density. Isn’t water vapor less dense than dry air, so humid air has lower density than dry air?
Dispy from Poughkeepsie
Dear Dipsy,
Technically, you are right, if by technically, you mean absolutely and without any reservation. When I look at the psychrometric chart again, I clearly see that as the relative humidity goes up, the density of the mixture of air and water vapor goes down.
This sounds like it would be a good bar bet, because I was surprised to find this out. I always thought that humid air was more dense than dry air. Maybe it’s just intuition, because damp things weigh more than when they are dry (like laundry). I asked three other thermal “experts” whether humid air was denser than dry air, and they all immediately said the same thing: the wrong thing. One even made me show him the psychrometric chart before he would pay off on the bet.
The main point of my article does not change, though. The affect of humidity on component temperatures is still negligible, because the amount of water in even very humid air is still very small, and only changes the density by a tiny percent. I was just right in the wrong direction this time.
—————————————————————————————————————
Dear Mr. Nusselt,
At the end of your excellent November 2001 article about humidity, air density, and its affect on heat transfer, you made another small boo-boo. You said that convection heat transfer would be different at 50C ambient than at 20C ambient, because the temperature change reduced the air density by about 10%. Well, true, the density does go down with temperature, but the conductivity of air increases with temperature, and just about cancels out any change in the Nusselt number.
Jimmy from Metropolis
Dear Mr. Olsen,
OK.
I knew I should never have written an article about the Nusselt Number. I said that when the air density changes, the Nusselt Number changes, as in this equation:
Nu = C Rem Prn
because the Reynolds Number (Re) has density as one of its terms. And when the Nusselt Number (Nu) changes, the heat transfer coefficient (h) changes, too, because
Nu = (h L)/ k
where L is a length scale and k is the conductivity of the air. But sure enough, k is not constant with temperature! It is with pressure, so what I said about altitude is still true. But if the air temperature changes, the density goes down and k goes up, and the value of h stays pretty much the same.
So it is pretty safe to measure the temperature rise of a component at 20C ambient, and that temperature rise should stay the same, even at an ambient of 50C. This agrees with my experience, except when power dissipation is a function of temperature, which is a whole different article. You can correct me on that one when I write it next month.
—————————————————————————————————————
Isn’t Everything He Knows Wrong, Too?
The straight dope on Tony Kordyban
Tony Kordyban has been an engineer in the field of electronics cooling for different telecom and power supply companies (who can keep track when they change names so frequently?) for the last twenty years. Maybe that doesn’t make him an expert in heat transfer theory, but it has certainly gained him a lot of experience in the ways NOT to cool electronics. He does have some book-learnin’, with a BS in Mechanical Engineering from the University of Detroit (motto:Detroit— no place for wimps) and a Masters in Mechanical Engineering from Stanford (motto: shouldn’t Nobels count more than Rose Bowls?)
In those twenty years Tony has come to the conclusion that a lot of the common practices of electronics cooling are full of baloney. He has run into so much nonsense in the field that he has found it easier to just assume “everything you know is wrong” (from the comedy album by Firesign Theatre), and to question everything against the basic principles of heat transfer theory.
Tony has been collecting case studies of the wrong way to cool electronics, using them to educate the cooling masses, applying humor as the sugar to help the medicine go down. These have been published recently by the ASME Press in a book called, “Hot Air Rises and Heat Sinks: Everything You Know About Cooling Electronics Is Wrong.” It is available direct from ASME Press at 1-800-843-2763 or at their web site at http://www.asme.org/pubs/asmepress, Order Number 800741.