Answers to those Doggone Thermal Design Questions
By Tony Kordyban
Copyright by Tony Kordyban 2001
Dear Thermal Answering Man,
I did a thermal test at room temperature (around 21 deg C) and at 55% Relative Humidity (RH) and I got a component temperature of 49 deg C. That seemed good because the component is rated for 85 deg C maximum.
But what I really need to know is the component temperature when the ambient is 50 deg C and 23% RH. How do I extrapolate my test results to this condition?
If the only change is from 21 to 50 deg C, then I would simply add the difference (50-21=29 deg C) to 49 deg C (29+49=78 deg C). I would then compare 78 deg C to the 85 deg C limit, and everything is still OK.
But how do I handle the moisture content change? By increasing the Specific Heat (Cp) value? By how much?
I expect that higher moisture incoming air would lead to better cooling. But is the effect negligible? Especially between 55% RH and 23% RH?
Sweatin’ It Out in Watervliet
Dear Sweat,
What an excellent question, which I swear I did not make up myself, this time. I have always just assumed that relative humidity didn’t affect air cooling of electronics very much, but I never sat down to verify whether that assumption holds water. The non-heat-transfer-understanding-type person thinks that high humidity makes things hotter, because we feel hotter when the humidity is high. But that is only because when the air is already full of water, our sweat can’t evaporate to cool us by absorbing the heat of vaporization from our skin. But unless your components have sweat glands, that has nothing to do with your question.
Specific heat (Cp) changes with humidity, but I don’t think we care about that, unless all we want to know is the temperature rise of the air instead of the components. Where I think humidity affects convection is that the water vapor increases the density of the air. In general, the higher the density of the fluid, the better the convective heat transfer. The question is, how much better? To find out, I cracked open a textbook on convective heat transfer. Unfortunately, the answer is not as simple as one would like, for the purposes of a short, entertaining column like this. But here goes anyway. There are lots of empirical relationships for convective heat transfer, and they all have a form similar to this:
Nu = C Rem Prn
where Nu is the Nusselt Number, Re is the Reynolds Number, and Pr is the Prandtl Number. I swore I’d never write an article using the Nusselt Number, but, darn it all to heck, there’s no way out of it this time.
Let’s start by getting rid of the Prandtl Number. It is a property of the fluid, and since we are talking about air in both cases (as opposed to maybe comparing air to liquid sodium), Pr doesn’t change, so we can just ignore it completely, along with its little bothersome exponent “n”. (Maybe Pr does change a little with humidity, but let’s not get into that.)
The Nusselt Number is a dimensionless form of the heat transfer coefficient (h), given by
Nu = (h L)/ k
where L is some length scale of the problem and k is the thermal conductivity of the fluid.
The Reynolds Number is another dimensionless number defined as
Re = (velocity x density x L) / viscosity
C, m and n are “constants” that change depending on the flow situation, such as whether it’s in a duct or over a flat plate or through pipe bundles, whether you have turbulent or laminar flow, constant flux or isothermal surfaces, and on and on. Every little situation has its own set of C, m and n. For our purposes, all we really need to care about is m, and you’ll soon see why.
Why do we even need to bring up the Nusselt Number? You asked how component temperature varies with Relative Humidity. Here is how I will try to connect the dots: component temperature depends on the heat transfer coefficient, the heat transfer coefficient depends on Nu, Nu depends on Re, and Re depends on density, and finally, density depends on humidity. Got that?
Now I’m going to speed up a little, because equations get boring real fast. Here is the basic equation for the temperature rise of your component above the ambient:
temperature rise = Power / (h x Area)
Let’s divide the temperature rise at one relative humidity by the temperature rise at another, to get this:
(temperature rise2 / temperature rise1) = (h1 / h2)
Notice how conveniently the Power and Area cancel out. The same thing happens when we throw in the Nusselt Number expression for h. All the constants, the length scales, the velocities, the viscosities all cancel out, assuming that they don’t change with humidity. (This analysis only applies to fan cooling, not natural convection. I am assuming you have a fan cooled system, since you didn’t tell me.) The only thing left is the density, which we assume is not constant with humidity, and the exponent “m” that goes along with it.
(temperature rise2 / temperature rise1) = (density1 / density2)m
What does this mean? It means, in general, as the density goes down, your temperature rise will go up. How strong this function is depends on the value of the exponent “m”. If m is a big number, the function is strong. If m is 1, then the temperature rise is inversely proportional to the density. If m is 2, then temperature will increase much faster.
In the textbooks I checked, m ranges from 0.2 to 0.8. That means the function is weaker than being inversely proportional. Let’s assume the worst, that m = 0.8. If the density decreases by 50%, the temperature rise will increase only by 38%.
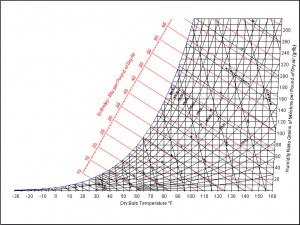
Now we think we have a handle on how component temperature changes with density (if you believe any of that Nusselt Number/ Reynolds Number stuff.) But how does air density change with Relative Humidity? This part is not so simple either. There isn’t a simple equation. It is time for the big trick of the show — the Psychrometric Chart.
When I was a college kid, all the engineers had a textbook with a fold-out, and not the full-color, airbrushed kind. Thermodynamics texts had a Psychrometric Chart in the back, that look like this:
Since water vapor in air behaves very little like an ideal gas, we needed such a chart to find the properties of humid air. Don’t worry, you won’t have to learn to read such a monster — it has all been computerized for you. (Check out www.parkssoft.com/ez_info.html or www.linric.com/webpsysi.htm for examples.) From my faded and yellowed chart that I dug out of the appropriately damp basement, I find the water content of air in your two cases to be:
| Case | Temperature | R.H. | kg H2O / kg dry air |
| 1 | 21 | 55% | 0.0086 |
| 2 | 50 | 23% | 0.017 |
At 50C and 23% R.H. there is actually twice as much water in the air then at 21C and 55% R.H. So the air is denser at your higher ambient. Not what you expected, eh? (Me neither.) So the heat transfer will work a little better in Case 2 than in Case 1. How much better?
There is also surprisingly little water in the air, so when it doubles, it doesn’t have much effect on the overall density of the air/water mixture. The change in air density between Case 1 and Case 2 due to water vapor is about 0.8%.
If you use the highest value of m to get the change in component temperature rise, you would get a reduction of about 0.6%. In your example the temperature rise was 28 degrees. The change due to humidity would be about 0.2 degrees C.
So you can pretty much forget about the Relative Humidity. It is probably smaller than your experimental error. (As Van Johnson says, in my favorite line from Brigadoon, “It’s not the heat, it’s the humanity.”)
But now that you brought up the subject, I can’t let you off the hook so easily. You were worried about humidity, but you didn’t even ask about the change in air temperature itself.
[2012 Update: alert readers sent in a correction after this article was first publsihed in 2001. Adding water vapor to air actually reduces its density, because water vapor is less dense than dry air. So the higher the Relative Humidity, the lower the density, the worse the convection, and the higher the component temperature. The effect is still small enough to forget about, but we might as well get the physics right.]
According to the Ideal Gas Law, when air temperature goes up from 21 deg C to 50 deg C (actually, from 294 to 323 K), its density goes down about 10%. That’s an order of magnitude bigger than the change due to humidity. Following my Nusselt Number argument, that could lead to an increase in component temperature rise as much as 7.8%, or about 2 degrees C, in your example.
Forgot the Ideal Gas Law? Here is the version you need:
(density2 / density1) = (T1 P2) / (T2 P1)
where T is absolute temperature, and P is pressure.
Pressure! You didn’t forget the pressure, did you? Did you record the barometric pressure at the time and location of your test? Density is directly proportional to the pressure, which can vary about 5% due just to changes in the weather. And, of course, it varies with altitude. What is the highest altitude at which your product is supposed to work? Better find out. That has the biggest affect on density of all these factors. For example, the density decreases by nearly 50% when you go from sea level to 13,000 ft.
But, other than that, just go ahead and add the difference between your test ambient and 50 deg C to your component temperature. Feel any less sweaty yet?
[Another 2012 update: Another alert reader explained that I forgot to mention that the conductivity of air increases with temperature. The increase in conductivity tends to cancel out the decrease in density, so that the convection itself does not change much as the ambient temperature goes up.]
—————————————————————————————————————
Dear Tony,
That Nusselt Number stuff is very convincing. It’s always hard to argue with an equation that has fractional exponents. Is there any experimental evidence that says that component temperature increases with the fractional power of the air density?
Skeptic from Missouri
Dear Skep,
There are a few articles that give methods of correcting temperatures for different altitudes (which is the same thing as density.) They give pretty much the same reasoning about Reynolds and Nusselt Numbers, with some other wrinkles thrown in. Some even give specific correction factors to predict component temperatures at different altitudes. But none are backed up by any experimental data, as far as I know.
I have done a few simplistic tests on real circuit boards in altitude chambers. They seem to suggest that component temperature depends on more than just the change in density. All temperatures do increase as the density decreases. But many of the components did NOT increase as much as the Nusselt Number method would suggest, and I don’t know why. None increased MORE than the Nusselt Number method predicted. So the method is conservative, and, so far, it’s the only thing I have to work with.
Sounds like a good research project for a university that has an electronics cooling program and an aeronautical engineering lab that might have a low pressure wind tunnel. Any body interested? I’ll kick in $75 from my research support budget.
—————————————————————————————————————
Isn’t Everything He Knows Wrong, Too?
The straight dope on Tony Kordyban
 Tony Kordyban has been an engineer in the field of electronics cooling for different telecom and power supply companies (who can keep track when they change names so frequently?) for the last twenty years. Maybe that doesn’t make him an expert in heat transfer theory, but it has certainly gained him a lot of experience in the ways NOT to cool electronics. He does have some book-learnin’, with a BS in Mechanical Engineering from the University of Detroit (motto:Detroit— no place for wimps) and a Masters in Mechanical Engineering from Stanford (motto: shouldn’t Nobels count more than Rose Bowls?)
Tony Kordyban has been an engineer in the field of electronics cooling for different telecom and power supply companies (who can keep track when they change names so frequently?) for the last twenty years. Maybe that doesn’t make him an expert in heat transfer theory, but it has certainly gained him a lot of experience in the ways NOT to cool electronics. He does have some book-learnin’, with a BS in Mechanical Engineering from the University of Detroit (motto:Detroit— no place for wimps) and a Masters in Mechanical Engineering from Stanford (motto: shouldn’t Nobels count more than Rose Bowls?)
In those twenty years Tony has come to the conclusion that a lot of the common practices of electronics cooling are full of baloney. He has run into so much nonsense in the field that he has found it easier to just assume “everything you know is wrong” (from the comedy album by Firesign Theatre), and to question everything against the basic principles of heat transfer theory.
Tony has been collecting case studies of the wrong way to cool electronics, using them to educate the cooling masses, applying humor as the sugar to help the medicine go down. These have been published recently by the ASME Press in a book called, “Hot Air Rises and Heat Sinks: Everything You Know About Cooling Electronics Is Wrong.” It is available direct from ASME Press at 1-800-843-2763 or at their web site at http://www.asme.org/pubs/asmepress, Order Number 800741.