Answers to those Doggone Thermal Design Questions
By Tony Kordyban
Copyright by Tony Kordyban 2004
Esteemed Dr. Kordyban,
What is the current carrying capacity for different wire gauges? Also, what copper trace thickness is required in a printed circuit board for each level of electrical current? Component power keeps going up, while the voltage levels are going down. That means higher and higher current flowing in the copper traces. I’m starting to worry the board is going to burn up before the components.
I used to have an old chart of the current capacity of wire gauges. It was a copy of a fax of a page torn out of a somebody’s lab notebook, but I can’t lay my hand to it anymore. Can you give some up-to-date guidance, or at least help find the original source for that current/gauge chart?
Wired in Coffeeville, Kansas
Dear Wired,
At the risk of losing my credibility, such as it is, please don’t call me Doctor. I did not go to medical school, nor earn a Ph.D. in any field. Neither did I grow up in the southern US, where they sometimes throw around honorary titles like “Colonel” and “Judge.” My dad was Dr. Kordyban, a professor of mechanical engineering, but if you need an answer from him, you will have to ask your Internet Service Provider to sign you up for Celestial E-mail. He has been teaching Fluid Dynamics at the Campus Eternal since 1996.
I have to disappoint you about the current/wire gauge chart, too. I don’t have a source for one that I actually believe in. I have seen examples of the second-hand design guide you mention, but I don’t know what they are based on. When I see people designing sophisticated electronic products using undocumented rules of thumb, I cringe. I hate rules of thumb.
Big Disclaimer: If you are designing wiring that is required to conform to local or national electrical codes, please please please PLEASE follow the applicable code that tells you what size wire to use for your current. These safety codes are based on lots of testing and years of experience with how bundles of wiring behave in conduits running through buildings. Don’t try to second-guess the electrical code based on what I am about to tell you in the rest of this article.
I was thinking about your question while making dinner. My wife likes spaghetti. I prefer angel hair pasta (a very thin form of spaghetti), for one very important technical reason. Spaghetti takes 8 minutes to cook, but angel hair takes only 3 minutes.
The fatter the noodle, the longer the cooking time. I knew that from experience (and from reading the instructions on the side of the box.) But I began to wonder if there were a physical reason for it. There are plenty of unscientific practices in cooking, and pasta boiling times could easily have been one of them. But not this time! If you look at the math, it becomes quite obvious why the skinnier pasta cooks faster.
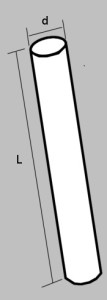To become cooked to the magical state called al dente, the mass of the noodle must be raised from room temperature to the protein softening temperature. (The cookbooks don’t tell you this temperature, because you can’t measure it during the cooking process anyway.) The mass of the noodle is given by
M pasta = r L p d 2 / 4
where
Mpasta is the mass
r is the density of pasta (which I assume is constant for all pasta, fat or thin)
L is the length of the noodle
d is the diameter of the noodle
The speed at which heat will get into that mass of pasta is directly related to the surface area of the noodle that is in contact with the boiling water. Whether we are talking about natural convection, forced convection, or boiling heat transfer, the rate of heating is always directly related to the surface area. The more surface area, the faster the heating.
For cylindrical pasta such as spaghetti and angel hair, the surface area (A) is given by
A = L p d
For fast cooking time, the pasta should have lots of surface area for a given mass. Dividing the second equation by the first gives us the ratio of area to mass for any cylindrical noodle.
Heating speed metric = 4 / (r d )
The smaller diameter noodles do have more surface area per kilogram than their fatter cousins, and so it is logical that angel hair pasta cooks faster than spaghetti. (When I told my wife about this, her first reaction to my analysis was “What about linguine?”) The larger the diameter of the noodle, the slower the cooking, because the mass increases more than the surface area.
That made me wonder a little bit more about your wire gage problem. Because if skinny noodles heat up faster than fat ones, wouldn’t they also cool off faster? The heat transfer equations are reversible. If you dunked hot angel hair into cold water, it would cool off faster than a similar mass of fatter spaghetti.
So if skinny noodles cool better than fat ones, why not electrical wires? Don’t smaller diameter copper wires have more surface area per mass than larger ones? Then why are larger diameter wires needed for higher current?
As in the angel hair vs. spaghetti puzzle, I let the math tell me the story.
The first thing we need to understand is what we are trying to control by choosing a particular size of wire. I am pretty sure we are trying to limit the temperature of the wire so that the insulation does not lose its ability to insulate. And assuming we know the general environment where the wire will be used, we know the maximum ambient temperature. So what we really want to control is the temperature rise of the wire above ambient.
The cause for the wire to heat up is the electrical resistance of the wire itself as current passes through. This is given by
Q = I 2 R
where
Q is the heat generated inside the wire
I is the current
R is the resistance of the wire
For cylindrical wire, the resistance is related to dimensions of the wire by
R = 4 L re /( p d 2)
where re is the resistivity of the copper, a property of the metal (let’s assume it’s constant with temperature, which it is, close enough, when your are arguing that wires are like spaghetti)
That tells you about the heat generated inside the wire. How the heat gets out of the wire in steady state is given by the familiar convection equation:
Q = h A DT
or
Q = h L p d DT
where h is the coefficient of convection to the ambient.
In steady state, the heat generated by the current in the wire is equal to the heat lost to the ambient by convection (or some other process similar to convection.) So I’m going to combine the previous three equations:
Q = I 2 R = I 2 4 L /( re p d 2) = h L p d DT
After some simplification it boils down to an expression for the current allowed at a particular temperature rise:
I allowable = ( h re DT p2 / 4) 0.5 d 1.5
Amazing! The math agrees with what we’ve been taught all along. For the current to increase without increasing the wire temperature, the diameter of the wire has to go up.
There is one other factor in that equation that I need to point out. It is the reason I don’t like those standard charts and tables of wire diameter vs current. Remember h? The allowable current in the wire is also dependent on h, the convective coefficient from the surface of the wire to the ambient. Those tables and charts seem to forget about h. What if the wire was strung in a vacuum? What if there is an air flow of 1000 meter/second over the wire? What if the wire is suspended in boiling water, like my angel hair pasta? The value of h can vary tremendously, depending on your application.
If the convection from the wire can vary tremendously from one application to another, how can anybody give you a chart that says, “Here, use this wire diameter with this current, and the wire will never overheat! No matter what the cooling situation!”
This might sound like I’m trying to make your job harder. I suppose that rules of thumb are easier to follow than doing detailed analysis.
But I’m also giving you more freedom.
It is quite possible that those charts and rules of thumb were too conservative for your application. You might be able to use skinnier wires and printed wire traces than those old charts would allow, if you have a good cooling method.
Let’s say you have a lot of high power components on your board, so you went to a lot of trouble to provide a liquid-cooled cold plate in contact with the board. The effective value of h is extremely high. Why should you size the traces in your board according to some old chart that assumed h is a low value? Your traces are not likely to overheat when they are closely coupled to a liquid cold plate.
My advice is to think of the copper traces in your board as if there were any other component. The traces generate heat, and have operating temperature limits just like any microprocessor or optical transceiver. Size the traces based on the complete heat transfer environment.
It is more work to do it that way.
But you might as well learn how to do it. The current in circuit boards will soon get so high that rules of thumb just won’t work anymore anyway.
Next month : sauces!
—————————————————————————————————————
Isn’t Everything He Knows Wrong, Too?
The straight dope on Tony Kordyban
Tony Kordyban has been an engineer in the field of electronics cooling for different telecom and power supply companies (who can keep track when they change names so frequently?) for the last twenty years. Maybe that doesn’t make him an expert in heat transfer theory, but it has certainly gained him a lot of experience in the ways NOT to cool electronics. He does have some book-learnin’, with a BS in Mechanical Engineering from the University of Detroit (motto:Detroit— no place for wimps) and a Masters in Mechanical Engineering from Stanford (motto: shouldn’t Nobels count more than Rose Bowls?)
In those twenty years Tony has come to the conclusion that a lot of the common practices of electronics cooling are full of baloney. He has run into so much nonsense in the field that he has found it easier to just assume “everything you know is wrong” (from the comedy album by Firesign Theatre), and to question everything against the basic principles of heat transfer theory.
Tony has been collecting case studies of the wrong way to cool electronics, using them to educate the cooling masses, applying humor as the sugar to help the medicine go down. These have been published recently by the ASME Press in a book called, “Hot Air Rises and Heat Sinks: Everything You Know About Cooling Electronics Is Wrong.” It is available direct from ASME Press at 1-800-843-2763 or at their web site at http://www.asme.org/pubs/asmepress, Order Number 800741.