Answers to those Doggone Thermal Design Questions
By Tony Kordyban
Copyright by Tony Kordyban 2004
Dear TK,
How many grid cells do you use? Jerry says his typical thermal analysis uses between 50,000 and 100,000 grids, but Kim insists that if you don’t have at least a million cells in your CFD simulation, you might as well have just done a hand calculation. Since disk space, RAM, and even processor speed are so cheap and abundant these days, shouldn’t I be using as much grid as I can afford on every single problem and get the maximum possible accuracy? Is there still a good reason to use a coarse grid for anything? Is there such a thing a too much grid?
Bitsy from Manhattan
Dear Bitsy,
I use a lot of grid cells.
Realize that I started Computational Fluid Dynamics (CFD) for cooling electronics on a 33 MHz 486 PC with a whopping 8 MB of RAM. On that computer a problem with 100,000 grid cells could take three or four days to converge on a solution. So I still think 50,000 is a lot of grid cells.
Since I’m talking ancient history, let’s go back a little bit and explain what grid cells are in CFD and why it might be a good idea to use a lot of them.
In a cooling problem you generally want to figure out the flow of a cooling fluid, like air, and how much heat it carries away from solid heat sources, like electronic components, and what the temperature of those heat sources would be. If the geometry is incredibly simple, we could write equations for mass, energy, and momentum balance for the control volume, toss in some boundary conditions, solve them with a calculator, and be done with it. No grid cells.
By incredibly simple geometry, I mean something like a flat plate with uniform heat flux, parallel to the uniform flow in a wind tunnel. Or a round pipe with a uniform wall temperature.
Almost anything else is too complicated to write equations for that can be solved analytically. So we discretize the problem. We break the control volume surrounding our electronic assembly into a gazillion tiny pieces. The geometry and flow in each small piece is simple enough so that a set of energy, mass, momentum, etc. equations can be written for it. That gives us six or seven gazillion equations, and six or seven gazillion unknowns. Solving that is just number crunching and lots of tedious bookkeeping, for both of which computers are well suited.
These chunks, or pieces, are called grid cells. The grid comes from the fact that the numbers crunch a lot easier if the geometry of all the chunks are organized on some kind of regular grid pattern.
So why should more grid cells be better than fewer? With grid cells we are trying to approximate a smooth, continuous reality with a bunch of discrete, uniform blocks. Like making a model airplane out of Legos. The smaller the blocks are compared to the whole thing, the less we notice their blockiness. For example, how smooth and continuous does this photograph appear?
I bet you would like to have a few more pixels, or grid cells, to increase the resolution of the fine detail, so you could tell what this is a photograph of. Maybe, since this is an Internet article, a photo of a supermodel.
Let’s double the resolution.
You can start to make out some shapes. But even if you squint real hard you can’t tell if it’s a claw hammer or a butterfly emerging from a cocoon. You need more pixels.
Doubling the grid cells again helps a lot. You can now tell this is a photo of some kind of bonehead, although you might not be able to use this to ID somebody in a court of law. Let’s double it again.
You could keep increasing the grid cell number from here (in theory, at least, but this is as good as my cheap digital camera goes), but you probably have all the information you need at this level of resolution.
The same thing applies to grid cells in CFD. You can keep increasing the grid density forever, but at some point the increase in resolution does not give you any more useful information.
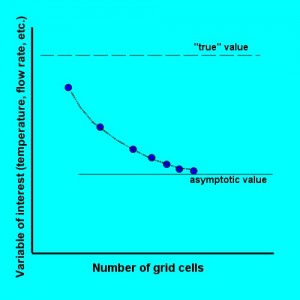
The general idea is that you want to use the number of grid cells in your problem that guarantee that the solution is Grid Independent. If you use a very coarse grid, you will still get a converged solution. But the temperature values for your electronic components may be suspect. So you increase the number of grid cells. If the temperature results change a lot when you increase the grid, then you can be sure your solution is not Grid Independent. Your results depend on the number of grid cells, so it is grid dependent. Keep increasing the number of grid cells until your results stop changing, as in this hypothetical chart.
If your results change appreciably when you add more grid, then you haven’t used enough grid. Keep adding grid until your results are close to their asymptotic value (they don’t change much anymore.) When that happens, adding more grid adds no more information. It just takes up more computing time and resources.
Notice that I didn’t say that Grid Independence gives you an accurate answer. My chart has a line marked “true” value. It can be very different from the asymptote, if there is some other source of error. Perhaps you entered 5 milliwatts instead of 5 watts for component power. All the grid in the world won’t make your results accurate. Grid Independence only eliminates the grid size as a source of error.
So now you think you know it all. Start with a coarse grid, and then keep adding more grid until the results stop changing. Grid Independence is the goal.
Not so simple, Bitsy.
There is such a thing as too much grid, maybe even before you achieve Grid Independence. It has to do with that dreaded topic — Turbulence Modeling and the Boundary Layer.
Some treatments of the boundary layer in CFD code expect you to add lots of grid next to solid walls, to resolve the velocity and temperature profiles inside the boundary layer. In that case, the more grid, especially right next to the wall, the better. The more detail you resolve in the boundary layer, the better your calculation of heat transfer will be.
But some treatments of the boundary layer, especially those that deal with turbulent flow, are smarter than that. They are built on the assumption that it takes too much grid to resolve the boundary layers everywhere. They try to capture the behavior of the boundary layer with just one layer of grid cells touching the wall, using a non-CFD technique called The Law of the Wall Theory. I won’t (and can’t) explain the Law of the Wall. Let me just tell you this about it: it assumes that the whole boundary layer thickness is contained inside the first layer of grid cells touching the wall. If the grid cells are smaller than the boundary layer thickness, then the Law of the Wall calculation doesn’t work properly. The wall friction and convective heat transfer and the wall temperature results won’t be accurate.
So study up on your turbulence treatments and make sure you understand the kind of grid each one needs. Some CFD codes offer half a dozen different methods of dealing with turbulence, and the grid requirements for each can be different. Making the grid too fine near the walls can lead to errors.
One final point: It’s not so important what the total number of grid cells is — its is more important to place them well.
Use lots of grid to resolve areas where the flow changes speed or direction rapidly, like where it comes out of a fan, or where it zooms around a sharp corner. Another place to load up on the grid cells is around a dense concentration of power, because the temperature is going to vary a lot over a small area. Use relatively coarse grid in areas where the geometry is uniform and smooth, and the flow does not change speed or direction. Here is another analogy:
Check out the dotted-line box in this photo. If we could add more resolution, would you rather add more inside the box, where all you will get is more uniform gray pixels, or would you rather add detail around something interesting, like the serrated edge on T-Rex’s tooth?
Selectively add grid where it will give more USEFUL information. That way, maybe you can get just as accurate, just as useful, just as grid independent results with 100,000 cells as Kim can get with his indiscriminate use of 1,000,000 grid cells.
—————————————————————————————————————
Isn’t Everything He Knows Wrong, Too?
The straight dope on Tony Kordyban
Tony Kordyban has been an engineer in the field of electronics cooling for different telecom and power supply companies (who can keep track when they change names so frequently?) for the last twenty years. Maybe that doesn’t make him an expert in heat transfer theory, but it has certainly gained him a lot of experience in the ways NOT to cool electronics. He does have some book-learnin’, with a BS in Mechanical Engineering from the University of Detroit (motto:Detroit— no place for wimps) and a Masters in Mechanical Engineering from Stanford (motto: shouldn’t Nobels count more than Rose Bowls?)
In those twenty years Tony has come to the conclusion that a lot of the common practices of electronics cooling are full of baloney. He has run into so much nonsense in the field that he has found it easier to just assume “everything you know is wrong” (from the comedy album by Firesign Theatre), and to question everything against the basic principles of heat transfer theory.
Tony has been collecting case studies of the wrong way to cool electronics, using them to educate the cooling masses, applying humor as the sugar to help the medicine go down. These have been published recently by the ASME Press in a book called, “Hot Air Rises and Heat Sinks: Everything You Know About Cooling Electronics Is Wrong.” It is available direct from ASME Press at 1-800-843-2763 or at their web site at http://www.asme.org/pubs/asmepress, Order Number 800741.
