Answers to those Doggone Thermal Design Questions
By Tony Kordyban
Copyright by Tony Kordyban 2003
Dear Tony the Thermal Tiger,
Where is the dividing line between conduction and convection in an air gap? I understand that when you have a trapped pocket of air that is very small, currents can’t form, and heat can only cross the air gap by conduction. And air is not a good conductor. But how small is small?
Let me tell you my real problem. I design electronics for military applications, which means the circuit boards are usually sealed up inside a metal box with no vents and no fans. The heat gets out by conduction through the board to the walls of the box, and from there to an external cold plate. Maybe there is some natural convection between the boards and the walls of the box. The air gaps in our boxes are usually between 1/4 and 1/2 inch.
My boss, who knows just enough about thermal to be dangerous, contends that in air gaps of that size the heat flow is always by conduction. I think that gaps any bigger than a 0.005 inch or so must have some kind of convection currents curling around in them. By the way, our boards are mostly vertically mounted. Does that make a difference?
Crackle from Battle Creek
Dear Crackle,
Your problem has been studied and answered more than 50 years ago, by, of all people, the folks in the home building industry. They needed to calculate the insulating value of double-wall house construction. If the inner plaster wall and the outer wooden wall are separated by a gap of 3 5/8 inches, does the air act as an insulator, or do circulation patterns develop inside the wall gaps? They asked the same questions about double-pane glass windows, trying the find the optimum gap between the sheets of glass to minimize heat loss. Little did they know that this would someday help in the design of a notebook computer or a power supply unit for a naval aircraft.
Here is the typical situation. There is a hot surface facing a cold surface across a closed-end gap. If the gap is small enough (and I will eventually tell you what small enough means), then you don’t have those curly arrows in the gap, which represent natural convection circulation patterns. The molecules of the gas still zip around in the gap. The difference is that their motion is completely random, and is constantly changing direction due to collision with other molecules. In conduction mode, heat gets across the gap from the hot surface to the cold one by the mechanism of air molecules randomly bouncing into one another, the hotter ones giving up energy to colder ones, until finally some hotter molecules bounce against the cold surface.
That mechanism is a lot different from convection. If the gap is big enough, the air can form large scale circulation currents that are not random, but organized. Air molecules near the hot surface pick up some heat, swing around the gap in the current, and then directly bounce against the cold surface and give up that heat. The rate of heat transfer in convection can be much higher than in pure conduction.
The mechanism that creates and drives the large scale currents is temperature-induced buoyancy. Hot air rises. Cold air sinks. They have different density, which get pulled on by gravity differently, so the air starts to move.
Now I can tell you what small enough means. In reality, the dividing line between conduction and convection depends on more than the size of the gap. It also depends on the temperature difference, because the temperature difference between the two surfaces drives the flow. It also depends on gravity, (so it is important that the surfaces are vertical!). And then there are those pesky details of the material properties of the fluid inside the gap.
When I start listing off all those things, you should start thinking Grashof number. Remember the dimensionless number that describes natural convection? There is a special form of the Grashof number for closed gaps. The characteristic length is the size of the gap, d.
Gr = g b (T hot – T cold) d3 / n 2
where:
g is the acceleration of gravity
b is the expansivity of the fluid
n is the kinematic viscosity of the fluid
Then we have the Prandtl number, another fluid property. For air it is about 0.7.
It is the product of the Grashof and the Prandtl number that determine the dividing line between conduction and convection.
There are actually three regimes:
1) When GrPr is less than 1000, there is pure conduction in the gap. Because natural convection is a cantankerous, unstable thing, the fluid in the gap can sometimes stay in pure conduction all the way up to GrPr of 10,000. Above that value the fluid has to start moving in the laminar flow regime.
2) When 10 4 < GrPr < 10 7, you can find the rate of heat transfer across the gap from this correlation:
Nu = 0.42 (Gr Pr) 0.25 Pr 0.012 (L / d ) -0.30
Remember Nu, the Nusselt number? It is the ratio of convection to conduction in a fluid. If Nu is equal to 1.0, then there is pure conduction.
Nu = h d / k in the situation of the gap,
where h is the convective heat transfer coefficient
and k is the conductivity of the fluid
and just in case you need this very last equation:
Heat transfer across the gap = h (Area of one surface) ( T hot – T cold )
3) If the gap keeps getting wider and wider, or the temperature difference gets bigger and bigger, the flow changes from the laminar to turbulent regime. This happens when Gr Pr > 10 6.
In the turbulent regime, the convection currents are well defined. Heat transfer can be found from
Nu = 0.046 (Gr Pr) 0.33
I know you hate these dimensionless correlations. So here is an example worked out. It even has a couple of surprises.
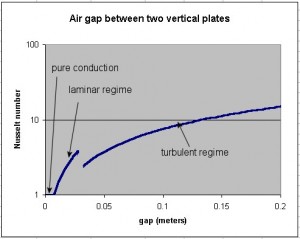Let’s say we have two walls, one at 50C and the other at 0C. That is in the range for an electronic enclosure. Then let’s see how the Nusselt number changes as we increase the gap from very small (1 mm) to very large (200 mm). For this example, L, the vertical dimension of the surfaces, is 250 mm.
In this example, for an air gap of up to about 6 or 7 mm, there is pure conduction, and the Nusselt number is 1.0. Up to a gap of about 20 mm, the convection is laminar, and at larger gaps, the flow is turbulent.
One mistaken impression you might get from this chart is that the heat transfer gets better and better as you increase the width of the gap. Don’t fall for that! It can be deceiving, because the Nusselt number includes the size of the gap in its definition. Let’s look at the actual heat transfer coefficient across the gap.
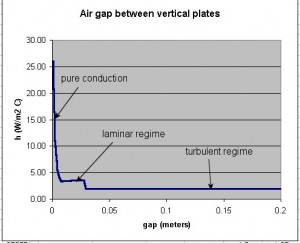The highest rate of heat transfer occurs when the gap is the smallest. This happens in the pure conduction regime. In this case, with this temperature difference, you actually get less heat transfer when the convection currents start moving. And there is less heat transfer across the turbulent gap than across the laminar gap. Also note that once the currents start to flow, h is a constant that does not change with increasing gap size. In the building industry, at least, this is important to know. Even if you make the wall thicker and thicker, you add no insulating value, if there is circulation inside the wall. (Normally, you’d expect a thicker wall to provide more insulation.) So make the wall thick, and stop the flow with barriers like fiberglass batting.
To answer your original question: you have gaps between 0.25 and 0.50 inches. That is in the range of 6 to 12 mm. If the temperature rise is 50C or less, then you probably are in the pure conduction range. You can find the value of Gr Pr that corresponds to your situation and decide for yourself.
Warning: This correlation is for surfaces at uniform temperature or uniform power dissipation. Your circuit boards are probably neither. Local temperature gradients on the surface of the board could cause natural convection to start up at lower values of GrPr than are given here. But this will give you a way to get a ballpark estimate.
—————————————————————————————————————
Isn’t Everything He Knows Wrong, Too?
The straight dope on Tony Kordyban
Tony Kordyban has been an engineer in the field of electronics cooling for different telecom and power supply companies (who can keep track when they change names so frequently?) for the last twenty years. Maybe that doesn’t make him an expert in heat transfer theory, but it has certainly gained him a lot of experience in the ways NOT to cool electronics. He does have some book-learnin’, with a BS in Mechanical Engineering from the University of Detroit (motto:Detroit— no place for wimps) and a Masters in Mechanical Engineering from Stanford (motto: shouldn’t Nobels count more than Rose Bowls?)
In those twenty years Tony has come to the conclusion that a lot of the common practices of electronics cooling are full of baloney. He has run into so much nonsense in the field that he has found it easier to just assume “everything you know is wrong” (from the comedy album by Firesign Theatre), and to question everything against the basic principles of heat transfer theory.
Tony has been collecting case studies of the wrong way to cool electronics, using them to educate the cooling masses, applying humor as the sugar to help the medicine go down. These have been published recently by the ASME Press in a book called, “Hot Air Rises and Heat Sinks: Everything You Know About Cooling Electronics Is Wrong.” It is available direct from ASME Press at 1-800-843-2763 or at their web site at http://www.asme.org/pubs/asmepress, Order Number 800741.