READ FOR FUN

Answers to those Doggone Thermal Design Questions

By Tony Kordyban

Copyright by Tony Kordyban 2003

Dear TK,

You preach that a person shouldn’t be allowed to practice cooling of electronics unless they can clearly explain the difference between heat and temperature to their mother-in-law.  I tried last Sunday over a chicken and dumpling dinner and got stuck.  I  wrote the equation for conduction on the tablecloth and got slapped on the wrist.  So then I launched into the old electrical analogy where voltage is temperature and current is heat, but it didn’t register with Ma.  How do you explain the difference between heat and temperature to your mother-in-law? 

Stuck washing dishes in San Jose

Dear Stuck,

Analogy is a powerful teaching tool, but it has one crippling weakness — the student has to be familiar with the thing you compare heat/temperature to, or it does no good at all.  The voltage/current analogy never did work for me, because Ohm’s Law was just one of those equations I memorized to pass a test.  I never developed an intuitive sense for electricity.

Even a really good analogy doesn’t work on everybody.  It has to be tailored to the audience.  Due to the complicated history of my wife’s family, I have three mothers-in-law.  I had to develop a different story for each of them.

In college I took a class that was team-taught by professors from every discipline in the engineering department.  One day a EE prof spent half an hour trying to explain the relationship between speed and torque in a pair of gears.  He said that the best way to understand how gears convert speed and torque was to think of them as a transformer converting voltage and current.  I nearly pulled out my hair (yes, I had some in college.)  Gears were obvious to me.  If you mesh a little gear to a big gear, the little one has to spin faster than the big one.  You can see it happening, even if it’s just in your head.  How did talking about a bunch of invisible lines of magnetic flux make it any more clear?  But as soon as he drew the chalk line connecting Gear Ratio to Turns Ratio, the EE students in the back of the room gasped, “Aha!”  So his analogy was helpful to somebody.

Here’s one that works for some of my mothers-in-law:

What is the difference between money and being rich?

Heat is like money.  It can flow from one body to another, and it can accumulate.  Like heat, it can move around, or be converted to something else, but it isn’t ever lost if you do your accounting properly.

If heat is money, then temperature is a measure of how rich somebody is, compared to somebody else.

Illustration:  Does a million dollars make one rich or poor?

Town A has a thousand citizens and Town B has ten citizens.  The federal government, being fair and benevolent, gives each town a grant of $1 million.  Both towns have received the same amount of money.  But which town now has richer citizens?

On average, Town A folks have $1,000 each.  Town B people, again on average, each have $100,000, so they are much richer than the people of Town A.  (In this way I want to get across the idea that temperature is, roughly speaking, the average amount of heat energy per molecule.  I say roughly, because molecules are obviously not all alike.  But in my analogy, molecules are represented by people.)

If you put the two towns in contact, which way will the money flow?  (This is where the analogy breaks down.  In real life, the rich people would find a way to get the poor people’s money away from them.  Perhaps that is an analogy for refrigeration.)  Being consistent with heat transfer theory, though, you have to assume that the richer you are, the more money you spend.  So if you put Town A and Town B in contact, money tends to flow from Town B to Town A until all the folks are equally rich (on average).  At equilibrium, each person would have $1980.

The rate at which money flows from Town B to Town A would be limited by how well the two towns were connected.  A poor connection would slow the flow.  This is similar to thermal resistance.

Try stretching the analogy further as your homework assignment.  What is the money analog for radiation?

Maybe the money/wealth analogy doesn’t work for you.  Maybe you have trouble balancing your checkbook and think money grows on trees.  You might prefer the scenario of water flowing through a pipe under pressure.  Or you could check out the exotic analogy in Chapter Four of my book, in which temperature is likened to the population density of crowd-hating monkeys on a tropical island.  Or temperature is like the Nielsen rating of a TV show, and heat is like … maybe not.

The point is that you need to have a clear picture in your own mind about this concept of flux, resistance and potential, before you start applying it to cooling electronics.  And the best way to learn something is to try to teach it to somebody else.  Now, if heat were similar to chicken gravy, what feature of the chicken and dumpling dinner would be equivalent to a 70 degree C ambient rated component?

—————————————————————————————————————

Dear Tony,

In engineering school, I thought that Murphy’s Law was an amusing exaggeration.  All the homework problems had workable solutions, so how hard could being an engineer be in the real world?  But after getting snagged into the job of cooling circuits, I soon learned that Murphy’s Law was just the beginning.  It seems that for every trick you think of to make temperature go down, Mother Nature has a trump card up her sleeve.  You know what I mean:  you add a thermoelectric cooler to refrigerate a hot chip, but that makes the heat dissipation triple and everything ends up hotter than before.  Are ALL the laws of nature stacked against us?

Pessimist from Murphysboro

Dear Pessimist,

There are a couple of examples I can think of where nature tries to help the struggling electronics cooling engineer.  One is natural convection.  When you increase the power, natural convection works harder (because the air flow is driven by the heat itself.)  In forced convection, if you double the power, the temperature rise doubles.  But in natural convection, when you double the power, the temperature rise only goes up by a factor of 1.7.  Don’t you feel lucky?

If you work a lot with natural convection, you might be familiar with my second example.  Because natural convection is a relatively weak form of heat transfer, radiation can play a large part.  It can be responsible for more heat transfer than natural convection itself, under the right conditions.

Figure 1. Radiation in a room.

Radiation is friendly to the thermal engineer in certain circumstances.  The one I am thinking of is when you have a sealed, heat-generating enclosure, such as a laptop computer, sitting on a bench in a large room.  Let’s ignore the possibility of the sun baking down on our little thought experiment.  In such a case, radiation is friendly, because as the ambient temperature goes up, radiation becomes more and more effective.  Assuming the power of our box is constant, that means as the ambient increases, radiation increases, and the box temperature rise above ambient would actually decrease, partially offsetting the increase in ambient.

As a pessimist, you probably assume the friendliness of radiation has got to be negligible.  Let’s take a look at a numerical example.

Figure 1 is a hot electronic box with a surface area of 1 square meter.  Let’s say it is painted with a really, really black paint so that its emissivity is 1.  It is completely surrounded by the walls of the room, and the walls are at the same temperature as the air.  The walls are also pretty good absorbers of infrared radiation, but that is not so important, as long as the room is much bigger than the box.  The ambient temperature of the room is stable, but from day to day it can vary from 0 C up to 50 C.

The net amount of heat given off by radiation from the box to the room is given by this equation:

Q _rad = S E A ( T_surface⁴ - T _ambient ⁴)

where:

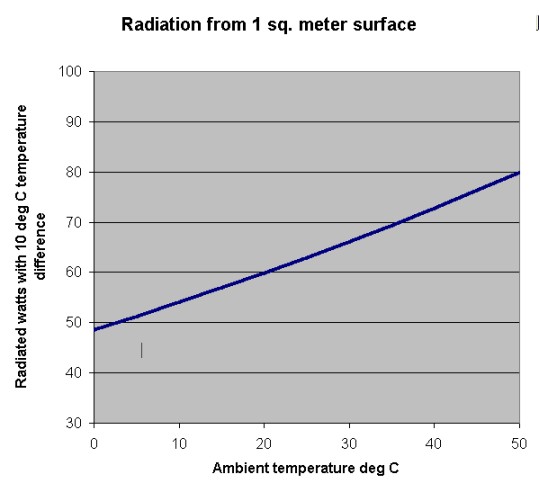
Everything in this equation is a constant except for the temperatures.  Unlike conduction or convection, radiation depends on the fourth power of the temperatures.  Not the temperature difference, but the difference of the fourth powers of temperature.  That gives radiation a behavior that is unexpected by those used to dealing with convection and conduction.  Radiation increases as the ambient goes up, even if the temperature difference between the two surfaces remains constant.

Let’s assume that the box surface temperature is 10 degrees hotter than ambient.  At 0 C ambient (273K), the box gives off 49 W by radiation.  At the maximum ambient of 50C, radiation increases to 80W (assuming the box temperature is still 10 degrees hotter than ambient.)  Over the operating ambient temperature range, radiation increases by about 60%.  That is not exactly negligible, especially when you consider how unfriendly nature has been to us in so many other areas.

—————————————————————————————————————

Isn’t Everything He Knows Wrong, Too?

The straight dope on Tony Kordyban

Tony Kordyban has been an engineer in the field of electronics cooling for different telecom and power supply companies (who can keep track when they change names so frequently?) for the last twenty years.  Maybe that doesn’t make him an expert in heat transfer theory, but it has certainly gained him a lot of experience in the ways NOT to cool electronics.  He does have some book-learnin’, with a BS in Mechanical Engineering from the University of Detroit (motto:Detroit— no place for wimps) and a Masters in Mechanical Engineering from Stanford (motto: shouldn’t Nobels count more than Rose Bowls?)

In those twenty years Tony has come to the conclusion that a lot of the common practices of electronics cooling are full of baloney.  He has run into so much nonsense in the field that he has found it easier to just assume “everything you know is wrong” (from the comedy album by Firesign Theatre), and to question everything against the basic principles of heat transfer theory.

Tony has been collecting case studies of the wrong way to cool electronics, using them to educate the cooling masses, applying humor as the sugar to help the medicine go down.  These have been published recently by the ASME Press in a book called, “Hot Air Rises and Heat Sinks:  Everything You Know About Cooling Electronics Is Wrong.”  It is available direct from ASME Press at 1-800-843-2763 or at their web site at http://www.asme.org/pubs/asmepress,  Order Number 800741.