READ FOR FUN

Answers to those Doggone Thermal Design Questions

By Tony Kordyban

Copyright by Tony Kordyban 2003

Dear Tony,

How fast does heat conduction go, anyway?

Here is the situation I’ve been thinking about.  Say there is a thick slab of something solid, like a big hunk of rock, or steel, and one side of it is facing thermal radiation, like the sun.  Forget about convection.  Say that it’s in a vacuum.

Suppose at the beginning the radiation is nice and gentle.  The radiation heats up the surface, and then the heat spreads down into the slab by conduction, so eventually the radiation heats up the whole slab.

In another situation the radiation might be a lot more intense.  Common sense tells me that the surface getting hit by the radiation will heat up a lot faster than conduction can spread it down into the rest of the slab.  If you really turn up the radiation, the surface will go way up in temperature and the inside of the slab won’t heat up at all.

That makes me curious about the time scale dependency of heat conduction.  Is there some time scale (milliseconds? nanoseconds?) at which heat conduction in a solid is negligible?
Jo-Jo from TableMesa

Dear Jo-Jo,

There are fundamental physical limits to how fast heat energy can get from place to place.  One is the speed of light.  Thermal radiation is the fastest, and it can’t go any faster than the speed of light.  If you are counting on heat energy getting from Point A to Point B any faster than that, you are out of luck, especially if you want it to pass through a solid.

Heat transfer through a solid obviously has to go a lot slower than the speed of light.  I don’t  know what the physical mechanism is in a solid that carries heat energy from one molecule to another.  Mechanical vibration?  In that case it might be limited by the speed of sound in that material.  Movement of free electrons?  Is it a cascade of thermal radiation from one molecule to the next?  In that case the speed could be anything between the speed of sound and the speed of light.

What would happen if you wanted to invent a thermal telegraph?  Say you had a long, insulated copper wire, and you wanted to send signals from one end of the wire to another by sending pulses of heat instead of electricity.  How fast would a pulse of heat travel down the wire?

An interesting question.  Perhaps even more interesting than the one you asked.  The explanations of heat conduction in an undergrad text don’t really deal with that stuff.  They assume that if you put some heat into a solid at one point, that it has an instantaneous effect on all the points in the solid.  Not very large right away. Any measureable temperature changes are delayed by the macro-scale things I’ll talk about a little later.  Perhaps this will be a topic for another day, when I learn something about it.

I don’t think the physics of thermal telegraphy is what you are worried about.  We don’t have to talk about nanoseconds to experience what you are talking about.  Everybody knows what happens when you cook a frozen hot dog in a frying pan.  If you turn up the heat too high, the outside of the hot dog will burn before the inside begins to thaw.  If you keep the flame low enough, you can get the inside to thaw and cook without burning the skin.  This happens on the scale of ordinary seconds and minutes.  It isn’t that conduction “turns off” or becomes “negligible” when the time scale is small.  Conduction heat transfer is proportional to the temperature gradient.  If you bombard the hot dog with a huge rate of incoming heat, it takes a large temperature gradient to conduct it.  Large gradient means that at one end you have a low temperature, and at the other end a very high temperature — a burnt skin on a frozen hot dog.

Figure 1.

But that doesn’t really tell the whole story at all.  There is a temperature gradient even in steady state conduction, when the temperatures are not changing with time.  You are asking about a transient problem, in which the temperature at any point in the solid is also changing with time.  So the temperature gradient itself also changes with time.

Maybe you’d be curious to know what kinds of things the transient temperature gradient depends on.  I know that your question has made me curious.  And when I get curious, you end up with an article, whether you are curious or not.

I love math.  I love equations.  I am not that good at math, and I am not especially good at solving equations.  The wonderful thing about engineering (and writing about engineering) is that you don’t always have to solve an equation for it to be useful.  Sometimes just the form of the equation tells you almost everything you want to know.

Equations for transient heat transfer are among the hardest I have ever had to try to solve, back in school.  I have vague nightmarish memories of Bessel functions connected to them.  Even so, let’s try to write an equation or two describing your slab heated by radiation.
To make things simple, I’m going to say that you have a semi-infinite slab, and that the radiation is uniform across the entire face of the slab.  By semi-infinite, I mean that the length and the width are very, very large, so that the edges are so far away that they don’t have any effect on a little piece in the center of the slab.  It is only “semi” -infinite, because it has a definite face where the radiation strikes it, and a finite thickness.  The beauty of this assumption is that it makes the problem one-dimensional.  Heat will conduct in only one direction, from the surface being irradiated, through the thickness of the slab. Temperatures along planes parallel to the face are all uniform, so there is no heat flow in the length or width directions.

Not that I can’t handle conduction in all three directions, but the notation starts getting cumbersome for a web-based article.

My goal is to write an energy balance for a couple of small chunks of the slab.  By “small” I mean that it is so small that you can say the temperature of the chunk is uniform, even though the temperature of the neighboring chunks are different.

For any chunk of the slab we can write an energy balance.  Here are all the possible heat transfer terms that might apply, although some of them might be zero for certain chunks.  First I’ll write it in words.

Radiation in + Heat conducted in – Heat conducted out = Change in internal energy / time

Internal energy is related to the change in temperature of a substance.

*  t has to be an appropriately small interval of time such that the change in temperature of the neighboring chunks is negligible during it.

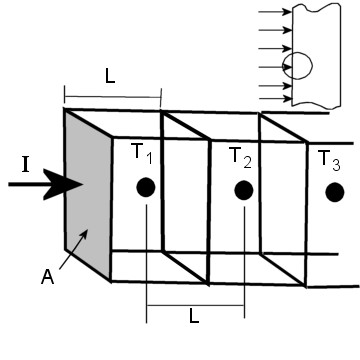
Figure 2. This figure shows how I have defined the geometry of the chunks of the semi-infinite slab. T1 is the temperature of the chunk at the surface being irradiated, T2 is the neighboring chunk inside the slab, and so on.

 
We are ready to write the energy balance equation for the chunk containing T₁.  It is a little different from all the interior chunks, because it alone will have a radiation term.

Q_rad + Q_cond = Q_int

 I A +  kA/L (T₂ – T₁) = (DT₁) A L d C_p / t

or                                     (DT₁) / t = { I + k/L (T₂ – T₁)} / (  L d C_p )

The energy balance for the chunk containing T₂ is very similar, and simpler.  Watch out for the plus and minus signs in these equations, if you ever get around to solving them!

Q_cond = Q_int

 kA/L (T₁ – T₂) + kA/L (T₃ – T₂) = (DT₂) A L d C_p / t

or                                      (DT₂) / t =  k/L (T₁ + T₃ – 2T₂)} / (  L d C_p )

All the interior chunks have the same equation as for T₂, except for the subscripts.  That is all you need to write.  Now, go ahead, start integrating already.  I’ll leave that part as an exercise for the reader.

Finished?

But I have already answered your question without solving the equations.  What I have done is written equations that tell you how fast the temperature of the solid changes at any particular location.  That is what  (DT₂) / t means — the change in temperature with time, or the speed at which solid temperature changes.  When you asked me “how fast does heat conduct?”, what you really wanted to know was how fast does temperature change at any spot in the slab.

Now you can look at the equations and get an idea what the speed of temperature change depends on.  For the surface chunk, it goes up with I, the intensity of the radiation, as your intuition would tell you.  But the rate of temperature change also depends on several material properties.  The speed goes up with k, the conductivity.  It slows down with higher density and higher specific heat.  Then there is a complicated dependence on the geometry of the problem.

So the burning hot dog does not depend on conduction “shutting off” at certain time scales.  It has to do with the relative values of the radiation intensity to the material properties of the solid, the ratio of the conductivity to the density and specific heat.  If you want to blast a slab with high intensity radiation, and have that heat conduct easily to the other side, pick a material with high conductivity, and low density and specific heat.

If you want to actually solve the problem for any particular geometry and material and level of radiation intensity, I suggest you use a finite difference thermal analysis program.  The programmers for commercial packages have already worked out the pesky plus and minus signs for you, and will give you nice color pictures of the temperature gradients as they form over time.

I will leave the equations unsolved as they are for now, and just look at them lovingly for a few hours more.

—————————————————————————————————————

Isn’t Everything He Knows Wrong, Too?

The straight dope on Tony Kordyban

Tony Kordyban has been an engineer in the field of electronics cooling for different telecom and power supply companies (who can keep track when they change names so frequently?) for the last twenty years.  Maybe that doesn’t make him an expert in heat transfer theory, but it has certainly gained him a lot of experience in the ways NOT to cool electronics.  He does have some book-learnin’, with a BS in Mechanical Engineering from the University of Detroit (motto:Detroit— no place for wimps) and a Masters in Mechanical Engineering from Stanford (motto: shouldn’t Nobels count more than Rose Bowls?)

In those twenty years Tony has come to the conclusion that a lot of the common practices of electronics cooling are full of baloney.  He has run into so much nonsense in the field that he has found it easier to just assume “everything you know is wrong” (from the comedy album by Firesign Theatre), and to question everything against the basic principles of heat transfer theory.

Tony has been collecting case studies of the wrong way to cool electronics, using them to educate the cooling masses, applying humor as the sugar to help the medicine go down.  These have been published recently by the ASME Press in a book called, “Hot Air Rises and Heat Sinks:  Everything You Know About Cooling Electronics Is Wrong.”  It is available direct from ASME Press at 1-800-843-2763 or at their web site at http://www.asme.org/pubs/asmepress,  Order Number 800741.