Answers to those Doggone Thermal Design Questions
By Tony Kordyban
Copyright by Tony Kordyban 2002
Dear Mr. High and Mighty,
I have to estimate the average natural convection coefficient variation around a short horizontal cylinder, at different altitudes, namely 50,000 feet and 80,000 feet. In heat transfer texts I found formulas for long isothermal horizontal cylinders which, in my opinion, could be sufficient for a rough first estimation.
The problem is Rayleigh and Prandtl number estimation at those altitudes: where I can get these?
Fox from Area 51
Dear Fox,
You will not find Rayleigh number as a function of altitude anyplace, because it is determined by your geometry as well a bunch of material properties and temperatures. But you can calculate it for yourself. The way you account for altitude is by plugging in the correct value of the air density into your calculation of the Rayleigh number.
Before the rest of you try to escape reading this by clicking on one of the nearby banner ads, let me see if I can spark your interest. Fox’s question gives an example of the power hidden in dimensionless numbers. Because the Rayleigh number is dimensionless, and more or less general purpose, you can use it to describe natural convection at different altitudes, where you might have a lot of trouble extrapolating dimensional test data to other altitudes.
Suppose Fox had found a paper giving the heat transfer coefficient for a cylinder, done at sea level and only one particular cylinder diameter. How much use would that paper have been for estimating the heat transfer coefficient at 80,000 ft for a much larger cylinder? But the correlation of dimensionless numbers that he did find in a text can be applied to any size cylinder, at any altitude, and maybe even for different fluids. So even though they are boring, dimensionless numbers can be extremely useful. If it helps to make them them more exciting, think of them as “The Numbers from Dimension Zero!”
Think way back to college, and maybe you remember the Reynolds number, and if you work with heat transfer at all, you might remember the Nusselt number. Those dimensionless numbers have two uses: 1) for estimating the convective heat transfer coefficient in forced convection, and 2) losing me lots of readers.
In natural convection, though, you don’t have fans pushing the air around. The temperature difference, combined with gravity, causes the air to change in buoyancy, and drives the flow. The kind of flow patterns and temperature gradients you get in natural convection are nothing like forced convection. So of course a bunch of different scientists got their names on the dimensionless numbers that describe it.
To estimate the natural convection heat transfer coefficient, you might use the Rayleigh number (Ra), which is based on the Grashof (Gr) and Prandtl (Pr) numbers like this:
Ra = Gr Pr
Pr is not strongly affected by altitude, so you can say it is constant for air at 0.7.
But the Grashof number is not so simple. It is defined like this (the formula was corrected in January 2005):
Gr = (g beta (Tw – Ta) x3) /(kinematic viscosity)2
| where | |
| g | is the acceleration of gravity |
| beta | is the volume coefficient of expansion of the fluid |
| Tw | is the wall temperature |
| Ta | is the air temperature |
| x | is the length parameter (length of a flat plate, for example) |
and kinematic viscosity = dynamic viscosity / density
Dynamic viscosity is not a function of density, but is just a property of air. So if you substitute dynamic viscosity into the Gr number, you will find it is a function of square of the density.
The Nusselt number is then a function of the Grashof number. The function depends on the geometry, which is the correlation you found in that textbook for long cylinders. After you find the Nusselt number, you can get the convective heat transfer coefficient from that.
Air density goes down with altitude, of course. You can find the density at each altitude in any mechanical engineering handbook, or look on the web if you don’t have a handbook.
The good news about natural convection at high altitude is that the heat transfer doesn’t degrade as badly as it does in forced convection. Because the flow is generated by the temperature difference, it tends to be self-correcting, in a manner of speaking. With a fan, you a stuck with a fixed volumetric flow, so the mass flow rate, and the heat transfer, goes down linearly with density.
But in natural convection, if the density goes down, the mass flow goes down, and the temperature difference goes up. But that forces the flow rate to increase, and partially compensates for the loss of mass flow.
So tell me, what kind of horizontal cylinder is just “floating around” at 80,000 ft? I assume that it’s not a rocket or airplane, because that would be moving pretty fast and not be subject to natural convection. Do blimps fly that high?
—————————————————————————————————————
Dear Mr. “CFD Solves Everything”:
Sometimes there is not enough time or need to do CFD analysis on every single electronic assembly. Are there any empirical equations, based on tests or experience, that one can use to obtain some reasonable values, particularly as related to forced convection? I know there is no magic wand covering solutions to problems in electronic cooling but I hope there are some magical equations that can provide the much needed information. Please also provide specific details about the documents that cover the requested information.
Quickdraw McGraw from Barberaville
Dear Quick,
I agree with you 100% that there is an important place for simple hand calculations in electronics cooling. They should be used for your first, second, and maybe your third cut at any problem, before you invest a lot of time in CFD modeling, that you could be using to watch sports on TV, or reading the letters between Vincent Van Gogh and his brother Theo to gain some insight into the genius and anguish that went into his paintings.
For example, my buddy Herb hands me a detailed drawing of a new circuit board with over 500 components on it. Before I start to model them in CFD, either in enormous detail, or with compact models, I do a simple “sanity check”. I phone my employer’s medical department to see if Herbie has gone off his medication lately.
“We’re not sure,” the doctor tells me, “How much power is he trying to cram onto a single board now?”
So I add up the power estimates for all the components: 400 watts (W).
What is the total surface area of the board? He gave me a 1 to 1 scale drawing, but I don’t happen to have a scale with me, so I estimate the dimensions by just spanning the drawing with my calibrated hand. About 200 mm wide by 300 mm long. Counting both sides of the board, that’s about 0.12 square meters of surface area.
In my industry, the inlet air temperature under worst case conditions is 50C. I’m pretty sure I never want the case temperature to get higher than 100C. Maybe I should really limit that to 85C, or even 70C. What I am picking here is what board temperature I could live with if the board were all at one temperature. Let’s pick 100C. I know that would be pretty unacceptable in real life.
What about heat transfer coefficient? You could use the flat plate correlations from any undergraduate textbook, if you want to get more detailed, if not more accurate. For my sanity check, I don’t bother. For natural convection, h is 6 W/mK. For fan cooling it is 50 W/mK. Maybe your fans work a lot better than mine. Great. Bump your value of h up to 100 if you like. I will use 50 to see what ballpark I’m in.
Then you plug numbers into the equation for convective heat transfer:
Q = h A (Tboard -Tair)
where Q is power, h is convective heat transfer coefficient, A is the total surface area, and T is temperature.
Get out your calculator and punch along with me. With Q =400W, I get an average board temperature of about 116C. That is pretty darn toasty. With that one calculation in hand, I go back to Herbie and tell him he needs either a bigger board, less power, or a lot more than the typical amount of air flow. Then I phone the medical department and have them up his dosage. And I didn’t even turn on my computer, except to see what’s happening on Goodreads, of course.
On the other hand, you want me to spell out for you all the handy equations I know about in a free advice column. That’s a pretty tall order. Not only would it take lots more space that I have in my column, but you are expecting an awful lot of help for free. The fact is that the kind of information you are looking for would fill up a book. And that book has already been written, probably more than once.
The one that I still like the best, even though it is out of print, is Gordon Ellison’s “Thermal Computations for Electronics.” See my column from April 2001 for some other books on the same topic.
—————————————————————————————————————
To My Electronics Cooling Hero:
Well, OK, then, how about a very specific question on hand calculation? I have a telecom shelf that I am planning to cool with fans. It is 4 RU high. Got any tables or equations or such that could help me estimate the pressure drop of the shelf full of circuit cards?
Boo-Boo from Jellystone Park
Dear Boo,
Happy to oblige. I use the number 14 to represent the flow resistance of “typical” telecom circuit boards. I derived this number years ago from a long forgotten experiment, and I have been using it ever since for estimating system pressure drop. Maybe the best value for you would be 10 or 20, depending on what “typical” means to you, but 14 seems to work for me. Whenever I try to come up with a refined value, I always get something like 13.9, so I just stick with 14.
“14 what?” you ask.
14 is the value for f in the following equation:
pressure / flow length = (f/2) (density) (velocity)2
Density is the density of air, in kg/m3. Velocity is the average air velocity flowing through the flow resistance, namely the shelf, in m/sec. The value 14 assumes you know the approach velocity, rather than the local velocity in some restricted channel inside the board slots. The flow length is the distance that the air flows through the flow resistance, in meters.
In your example, the shelf is 4 RU tall. In non-telecom talk, RU is a Rack Unit, equal to 1.75 inches. 4 RU is 7 inches, or 0.178 meters.
At an approach velocity of 1 m/sec (196 ft/min), the pressure drop is
pressure = (0.178m)(14/2)(1.16 kg/m3) (1 m/sec)2 = 1.4 Pascal
This is the pressure drop due to inlet and exit grills, board guides, and friction of “typical” components. It doesn’t include pressure drops due to air filters, sudden expansions or contractions, or 90 degree turns in the flow direction. You will find that those pressure drops are an order of magnitude larger than the drop due to the shelf and boards. You can find methods of estimating those pressure drops in the Gordon Ellison book I just told you about.
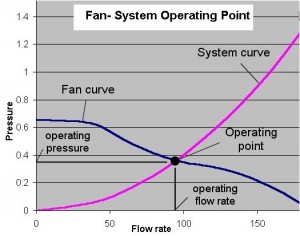
Using the number 14, you can generate a system resistance curve of Pressure vs Flow Rate. Remember that the volumetric flow rate is just the velocity times the cross-sectional area of the shelf. You can combine that with the performance curve of your fans, and get an estimate of the operating point, like this:
I hope that’s simple enough for everybody now. Throw away your CFD licenses. The heat transfer coefficient is always 50 and the flow resistance is always 14.
—————————————————————————————————————
Isn’t Everything He Knows Wrong, Too?
The straight dope on Tony Kordyban
Tony Kordyban has been an engineer in the field of electronics cooling for different telecom and power supply companies (who can keep track when they change names so frequently?) for the last twenty years. Maybe that doesn’t make him an expert in heat transfer theory, but it has certainly gained him a lot of experience in the ways NOT to cool electronics. He does have some book-learnin’, with a BS in Mechanical Engineering from the University of Detroit (motto:Detroit— no place for wimps) and a Masters in Mechanical Engineering from Stanford (motto: shouldn’t Nobels count more than Rose Bowls?)
 In those twenty years Tony has come to the conclusion that a lot of the common practices of electronics cooling are full of baloney. He has run into so much nonsense in the field that he has found it easier to just assume “everything you know is wrong” (from the comedy album by Firesign Theatre), and to question everything against the basic principles of heat transfer theory.
In those twenty years Tony has come to the conclusion that a lot of the common practices of electronics cooling are full of baloney. He has run into so much nonsense in the field that he has found it easier to just assume “everything you know is wrong” (from the comedy album by Firesign Theatre), and to question everything against the basic principles of heat transfer theory.
Tony has been collecting case studies of the wrong way to cool electronics, using them to educate the cooling masses, applying humor as the sugar to help the medicine go down. These have been published recently by the ASME Press in a book called, “Hot Air Rises and Heat Sinks: Everything You Know About Cooling Electronics Is Wrong.” It is available direct from ASME Press at 1-800-843-2763 or at their web site at http://www.asme.org/pubs/asmepress, Order Number 800741.