READ FOR FUN

Answers to those Doggone Thermal Design Questions

By Tony Kordyban

Copyright by Tony Kordyban 2002

Dear TK,

Here’s one for you. Lets assume that a chip on a circuit board can be approximated by a flat plate.  I know how to calculate all the necessary dimensionless parameters for heat transfer from a flat plate, so then I should be able to calculate the heat transfer coefficient, and from that, the temperature, but…

When I try it for free convection, the value I get for heat transfer coefficient does not agree with the case-to-air thermal resistance given by chip manufacturers. I figure out h (heat transfer coefficient) and I know the surface area of the component (A), so I assume that the thermal resistance from case to air (R_c-a) is just 1/hA.  But I don’t get anything close.   Is there a relationship I’m missing?

Flattop from Platteville

Dear Flat,

The missing link is that you studied heat transfer out of an engineering textbook and the guys who defined thermal resistance for electronic component packages didn’t.  But before I start ragging on those guys again, I need to point out a couple of problems with your first assumption:  that a component on a circuit board is like a flat plate.

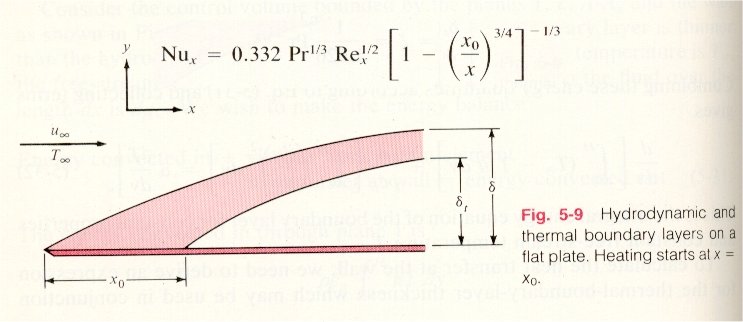
The textbook equations that I think you have been using (which use the dreaded Reynolds and Nusselt numbers which cause readers to quickly jump to some more entertaining web site) are for idealized flat plates.  The pictures in the books always show a very thin flat plate suspended by magic in an infinite sea of fluid (like air).  I suppose you could think of the top surface of a component package as being something like a flat plate.  But it doesn’t float in air by itself.  The closest you might get is to think of a component as being a small heated flat plate pasted onto a much larger unheated but thermally conductive flat plate representing the circuit board.  So already the equations might not apply to your geometry.

The textbook flat plates are always either isothermal or uniformly heated.  Isothermal means that the plate is all at one temperature.  I suppose a single component package might be isothermal on the surface.  But there is no way that you can assume that the circuit board is either isothermal or has uniform power dissipation, so those equations probably don’t apply because the temperature distribution is not the same as the flat plate in the textbook.

That’s because lots of the heat from the component package conducts through the leads into the circuit board and spreads out.  In natural convection up to 90% of the heat could be conducted into the board and only 10% given off to the air from the top surface of the package.  So the board is plate with a hot spot under the component with temperature gradients going off from it in all directions toward the edges.  Does that look like an isothermal plate to you?

So even if you can estimate a value for h (convection coefficient) from the flat plate equations, what value of area (A) should you use for calculating the heat transfer?  Heat is being convected off the component package and from the portions of the board that are hotter than the air.  So the effective area over which “h” is operating is somewhere between the area of the package and the total surface area of the circuit board.  That range of area could include two or three orders of magnitude, considering that the area of the board could be 1000 times as big as the package.

You said you wanted to estimate the value of R_c-a from 1/hA.  The concept is right.  But what is the correct value for A, the area that goes with h?

Not only will your value of thermal resistance be very unlikely to match the published value, but it won’t be of much use in calculating component temperature.

Now here are some reasons why the thermal resistances published in the data sheets won’t help you much either.

First, let’s explain how you got from a data sheet the value R_c-a, the thermal resistance between case and air, because that is actually not a value that anybody publishes.  They have R_j-a, the resistance between the junction and the air, and sometimes they have R_j-c, the resistance from junction to case.  It doesn’t take a genius to infer that

R_c-a =  R_j-a – R_j-c

assuming that the heat transfer from the junction to the ambient air is one-dimensional (which it ain’t!)  But if you believe you know the resistance between junction and air, and the resistance between junction and case, because somebody measured them according to some industry standard, then you can easily calculate the resistance between case and air.

There are two problems with how  R_j-a and R_j-c are measured:

• Thermal resistance of a component package is measured with that component soldered to a large circuit board (about 4 inches by 4 inches) all by itself.  Heat conducts into the copper in the board and is given off to the surrounding air.  The effective surface area can be over 100 times that of the component package itself.  When you use these values of thermal resistance, you have to understand that they also include the effects of a heat sink (the test board) that is not there in your application.
• The thermal resistances also include radiation losses.  When a circuit board is cooled by natural convection, as much as 50% of the heat can be given off as radiation.  This is true even in the test chamber.  Thermal resistances reported in the data sheet include all the heat lost from the package and the test board by radiation, as well as convection.  So Rj-a and Rc-a aren’t just measures of convection — they are measures of conduction, convection and radiation resistances all lumped together.  So they can’t be used to estimate convection coefficient (h) from a component package.  Radiation losses are lumped in, and you won’t know how to un-lump them out.

Conclusion:  You are not wrong when you find that flat plate equations for heat transfer don’t work when trying to estimate R_c-a for a component.  Why?  Because circuit boards are not isothermal flat plates, because the effective area  for convection from a package is probably not what you think it is, and because data sheet values of R_c-a include radiation losses.  It is kind of like you were taking a shot in the dark at a tiger, and the component folks were shooting at an elephant.  It’s no wonder your two bullets never came near each other.

Aren’t you glad you got into the business of trying to predict component temperatures?
—————————————————————————————————————

Hey Thermal Dude,

What scale is better, Fahrenheit or Celsius?  Seems to me that F degrees are more precise, because I saw in a Canadian doctor book that normal body temperature is supposed to be 37C, when everybody in the US knows that body temperature is 98.6°F.

Sun-baked in Sedona 

Dear Sun,

Personally, I prefer degrees K, but that is just a last-name thing.

Precision is in the eye of the beholder of the measuring instrument, not in the units.

The concept that 98.6°F is the normal body temperature for all people, and that 99°F is a mild fever is bogus.  The original studies that were done to determine normal body temperature reported the results in Celsius units, as 37°C, plus or minus 1°C. Some idiot converted 37°C using the formula F= C x 9/5 + 32 and got 98.6°.  To keep the same level of precision, he or she should have rounded it off to the same number of significant digits as the original data, and said that normal body temperature is about 99°F.

—————————————————————————————————————

Isn’t Everything He Knows Wrong, Too?

The straight dope on Tony Kordyban

Tony Kordyban has been an engineer in the field of electronics cooling for different telecom and power supply companies (who can keep track when they change names so frequently?) for the last twenty years.  Maybe that doesn’t make him an expert in heat transfer theory, but it has certainly gained him a lot of experience in the ways NOT to cool electronics.  He does have some book-learnin’, with a BS in Mechanical Engineering from the University of Detroit (motto:Detroit— no place for wimps) and a Masters in Mechanical Engineering from Stanford (motto: shouldn’t Nobels count more than Rose Bowls?)

In those twenty years Tony has come to the conclusion that a lot of the common practices of electronics cooling are full of baloney.  He has run into so much nonsense in the field that he has found it easier to just assume “everything you know is wrong” (from the comedy album by Firesign Theatre), and to question everything against the basic principles of heat transfer theory.

Tony has been collecting case studies of the wrong way to cool electronics, using them to educate the cooling masses, applying humor as the sugar to help the medicine go down.  These have been published recently by the ASME Press in a book called, “Hot Air Rises and Heat Sinks:  Everything You Know About Cooling Electronics Is Wrong.”  It is available direct from ASME Press at 1-800-843-2763 or at their web site at http://www.asme.org/pubs/asmepress,  Order Number 800741.